Oracle: Hash агрегация и приблизительный DISTINCT

Список статей о внутреннем устройстве Oracle:

Нововведение Oracle 12.1 - приблизительный подсчет уникальных значений ( APPROX_COUNT_DISTINCT ~= count distinct ).
Классический подход к расчету числа уникальных значений предполагает создание хэш массива, где ключ = колонке таблицы, а в значении число совпадений.
Число элемнтов в хэш массиве будет равно числу уникальных данных в колонке таблицы:

class RealDist {
 HashMap words;

 public RealDist() {
  words = new HashMap();
 }

 public void set(String word) {
  if (!words.containsKey(word)) {
   words.put(word, 1);
  } else {
   words.put(word, words.get(word) + 1);
  }
 } //set

 public int get() {
  return words.size();
 } //get
} // RealDist

Этот способ всем хорош, пока у нас достаточно памяти под хранение хэш массива.
При росте размера данных время и потребляемые ресурсы начинают катастрофически расти.

Пример со страницы antognini с разным числом уникальных значений на 10 млн. строк:

CREATE TABLE t
AS
WITH
  t1000 AS (SELECT /*+ materialize */ rownum AS n
   FROM dual
   CONNECT BY level <= 1E3)
SELECT rownum AS id,
    mod(rownum,2) AS n_2,
    mod(rownum,4) AS n_4,
   mod(rownum,8) AS n_8,
   mod(rownum,16) AS n_16,
   mod(rownum,32) AS n_32,
   mod(rownum,64) AS n_64,
   mod(rownum,128) AS n_128,
   mod(rownum,256) AS n_256,
   mod(rownum,512) AS n_512,
   mod(rownum,1024) AS n_1024,
   mod(rownum,2048) AS n_2048,
   mod(rownum,4096) AS n_4096,
   mod(rownum,8192) AS n_8192,
   mod(rownum,16384) AS n_16384,
   mod(rownum,32768) AS n_32768,
   mod(rownum,65536) AS n_65536,
   mod(rownum,131072) AS n_131072,
   mod(rownum,262144) AS n_262144,
   mod(rownum,524288) AS n_524288,
   mod(rownum,1048576) AS n_1048576,
   mod(rownum,2097152) AS n_2097152,
   mod(rownum,4194304) AS n_4194304,
   mod(rownum,8388608) AS n_8388608,
   mod(rownum,16777216) AS n_16777216
FROM t1000, t1000, t1000
WHERE rownum <= 1E8;

Скорость вычислений классическим способом падает вместе с ростом числа уникальных значений:

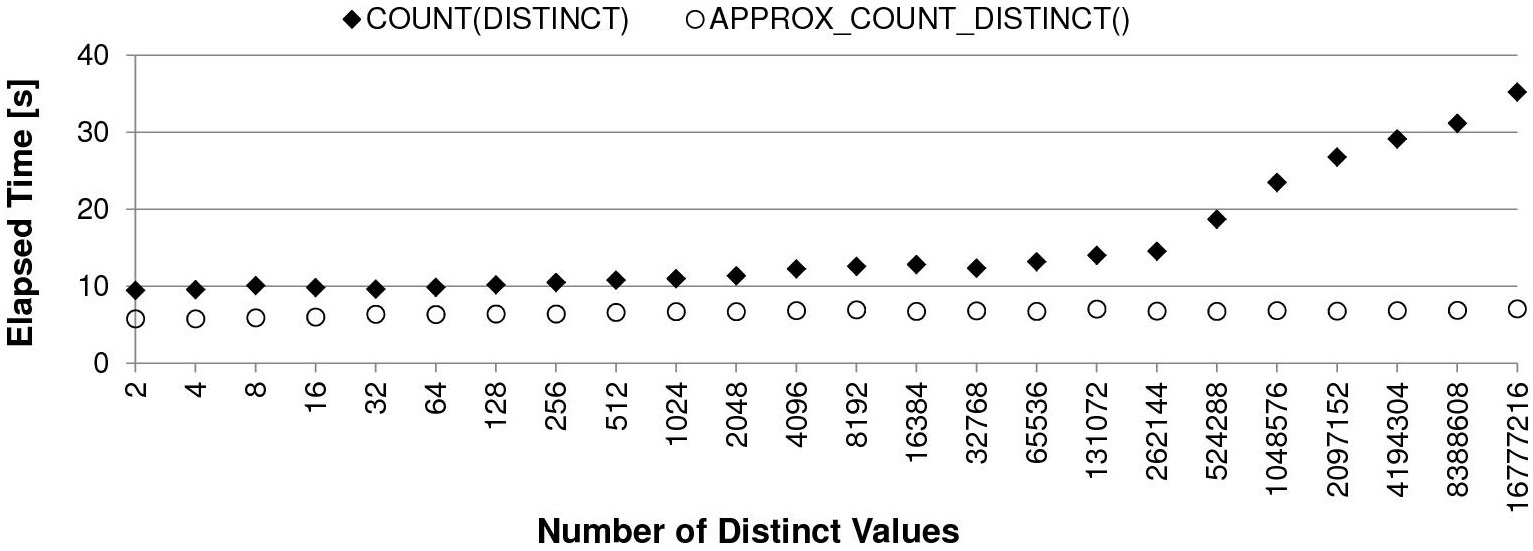
Пропорционально времени работы растет и потребление PGA памяти под хранение хэш массива:

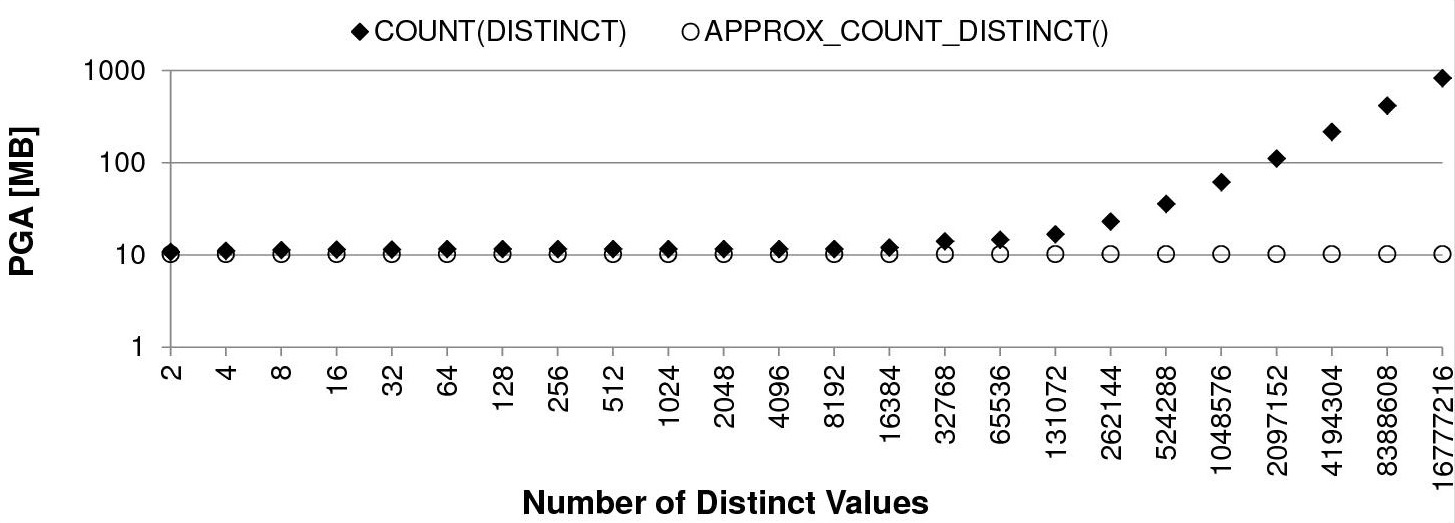
Чтобы решить проблему производительности/памяти и при этом получить приемлемый результат, можно применить приблизительный расчет числа уникальных значений.
Как и bloom filter он основан на вероятностных хэш значениях от данных.

Общий смысл приблизительного расчета (habr):

1. От каждого значения берется произвольная хэш функция

public static int fnv1a(String text) {
 int hash = 0x811c9dc5;
 for (int i = 0; i < text.length(); ++i) {
  hash ^= (text.charAt(i) & 0xff);
  hash *= 16777619;
 }
 return hash >>> 0;
} //fnv1a

2. У каждого хэш значения определяется ранк первого ненулевого бита справа.

// позиция первого ненулевого бита справа
public static int rank(int hash, int max_rank) {
 int r = 1;
 while ((hash & 1) == 0 && r <= max_rank) {
  r++;
  // смещаем вправо, пока не дойдет до hash & 1 == 1
  hash >>>= 1;
 }
 return r;
} //rank

Вероятность того, что мы встретим хеш с рангом 1 равна 0.5, с рангом 2 — 0.25, с рангом r — 1 / 2^ранг
Если запоминать наибольший обнаруженный ранг R, то 2^R сгодится в качестве грубой оценки количества уникальных элементов среди уже просмотренных.

Такой подход даст нам приблизительное число уникальных значений, но с сильной ошибкой.

Для данного алгоритма есть усовершенствованный вариант HyperLogLog:

а. От битового представления хэш берется 8 первых левых бит. Они становятся ключом массива (2^8 = 256 значений)

public void set(String word) {
 int hash = fnv1a(word);
 // убираем 24 бита из 32 справа - остается 8 левых
 // (=256 разных значений)
 int k = hash >>> 24;
 
 // если коллизия, то берем наибольший ранк
 hashes[k] = Math.max(hashes[k], rank(hash, 24)); 
} // count

б. Над массивов вычисляется формула:

где a_m - корректирующий коэффициент, m - размер массива = 256, M[] - массив ранков (hashes)

Для погрешности в 6.5% числитель этой формулы будет равен константе = 47072.7126712022335488.
Остается в цикле возвести 2 в -степень максимального ранка из каждого элемента массива:

public double get_loglog() {
 double count = 0;

 for (int i = 0; i < hashes.length; i++) {
  count += 1 / Math.pow(2, hashes[i]);
 }

 return 47072.7126712022335488 / count;
} //get_loglog

Данный алгоритм уже дает приемлемый результат на больших данных, но серьезно ошибается на небольшом наборе.
Для небольших значение применяется дополнительная математическая корректировка:

public int get() { 
 long pow_2_32 = 4294967296L;

 double E = get_loglog();

 // коррекция
 if (E <= 640) {
  int V = 0;
  for (int i = 0; i < 256; i++) {
   if (hashes[i] == 0) {
    V++;
   }
  }
  if (V > 0) {
   E = 256 * Math.log((256 / (double) V));
  }

 } else if (E > 1 / 30 * pow_2_32) {
  E = -pow_2_32 * Math.log(1 - E / pow_2_32);
 }
 // конец коррекции

 return (int) Math.round(E);
} //get

Проведенных тест на 1-2 томах войны и мира показал результаты:
* реальное количество уникальных слов = 3737
* приблизительное число уникальных слов основываясь только на максимальном ранке первого ненулевого бита справа = 16384
* приблизительное число уникальных слов по формуле из п. б на массиве из 256 элементов = 3676
* приблизительное число уникальных слов по формуле и корректировке = 3676

При ошибке числа уникальных значений в 6,1% мы затратили константное число памяти под массив из 256 элементов, что в разы меньше, чем при обычном хэш массиве.

Полный исходный код на java можно посмотреть на github

Скахин Алексей / pihel

Страницы

пятница, 17 февраля 2017 г.