Список статей о внутреннем устройстве Oracle:
Следующий важный аспект бд - индексирование данных в таблицах.
Раньше я уже описывал индексирование со стороны разработчика бд:
http://blog.skahin.ru/2015/04/oracle.html, сегодня копнем немного глубже, с кодом btree индекса на java.
B+Tree - Дерево поиска. С точки зрения внешнего логического представления, сбалансированное, сильно ветвистое дерево во внешней памяти.
Дерево (
BPTree ) состоит из корня (
root ), внутренних узлов (
INode ) и листьев (
LNode ), корень может быть либо листом, либо узлом с двумя и более потомками.
Сбалансированность означает, что длина любых двух путей от корня до листьев совпадает.
Ветвистость дерева — это свойство каждого узла дерева ссылаться на большое число узлов-потомков (
Node[] children ).
С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц внешней памяти, то есть каждому узлу дерева соответствует блок внешней памяти (блок / страница). Внутренние и листовые страницы обычно имеют разную структуру.
При этом данные хранятся только в последовательно связанных листьях (
LNode.next ), а в ветвях только ссылки на листья дерева (
INode.children ).

B-дерево может применяться для структурирования (индексирования) информации на жёстком диске. Время доступа к произвольному блоку на жёстком диске очень велико (порядка миллисекунд), поскольку оно определяется скоростью вращения диска и перемещения головок. Поэтому важно уменьшить количество узлов, просматриваемых при каждой операции. Использование поиска по списку каждый раз для нахождения случайного блока могло бы привести к чрезмерному количеству обращений к диску, вследствие необходимости осуществления последовательного прохода по всем его элементам, предшествующим заданному; тогда как поиск в B-дереве, благодаря свойствам сбалансированности и высокой ветвистости, позволяет значительно сократить количество таких операций.
Перейдем к особенностям реализации Oracle:
1. Т.к. бд хранит и считывает данные в
блоках/страницах, то размер листа/ветви = размеру блока. (
rows_block )
2.
Вставка
При достижении максимального числа элементов в блоке (
rows_block ) , лист должен разбиться на 2 части (
BPTree.Insert,
LNode.Insert ,
INode.Insert ), а копия среднего элемента перейти на ветвь выше (
Split ) рекурсивно (максимальное число ветвлений = 24. В Oracle этот параметр называется blevel (
BPTree.getBLevel) = height - 1 )
В Oracle реализован особенный алгоритм: если вставка элемента идет в крайний правый блок индекса (
Node.last), то разделение идет в соотношении
90/10.
Это значительно снижает размер индекса при вставке последовательных данных, т.к. данные в блоках получаются плотно упакованы.
Такая ситуация часто бывает на первичном ключе, генерируемый последовательностью.
Если вставка идет в середину индекса, то алгоритм стандартный - блок сплитится в соотношении 50/50, что приводит к появлению пустых мест и физическому разрастанию индекса на диске.
Пример индекса с числом элементов в блоке = 3:
* Вставка
последовательных данных: {1, 2, 3, 4, 5, 6, 7, 8, 9}
переполняющий элемент сразу идет в правый новый блок, не разделяя левый на 2 части:
1
2
3
. > 4
4
5
6
. > 7
7
8
9
( > - ветвь, . - высота ветви -- вывод функции
dump )
Всего 3 листовых блока и высота дерева = 2
* Вставка данных в
обратном порядке:
Массив из 3 элементов постоянно разбивается на 2 части:
1
2
3
. > 4
4
. > 5
5
. . > 6
6
. > 7
7
. . > 8
8
. > 9
9
Хороший визуализатор b+tree дерева можно видеть
тут
Тут ситуация хуже, индекс сильно разряжен: 7 листовых блоков и высота дерева = 3.
Индекс будет почти в 2 раза больше весить на диске и для обращений к нему нужно будет делать 3 чтения с диска, вместо 2 при последовательной.
Стоит заметить, что последовательная вставка в индекс это не всегда хорошо.
Если вставка преобладает перед чтением, то insert в разные части индекса лучше, чем последовательная в один блок. Т.к. это обеспечивает большую конкуренцию за общий ресурс и в итоге приведет к buffer busy wait. Специально для перемешивания данных используются реверсивные индексы (
http://blog.skahin.ru/2015/04/oracle.html).
3.
Поиск элемента
* начинаем с корня дерева (считываем его с диска) (
BPTree.indexScan )
* в блоке ветви бинарным поиском ищем элемент = искомому или первый больше его, если искомого нет в ветви (
INode.getLoc)
* если нашли, то спускаемся налево, иначе если искомый элемент больше максимального в блоке ветви, то двигаемся направо (считывание с диска) (
inner.children[idx])
* рекурсивно повторяем N раз = высота дерева - 1, пока не дойдем до листа (считывание с диска) (
LNode leaf)
* в упорядоченном массиве блока листа бинарным поиском (считывание с диска) (
leaf.getLoc)
Итого элемент будет найден за число считываний с диска = высоте дерева. Затраты CPU = высота дерева * log2(число строк в блоке)
3.
При удалении данных из индекса, в целях ускорения, элемент физически не удаляется, а лишь помечается удаленным. Тем самым индекс не становится меньше весом.
Для устранения эффектов из п. 2 и 3 индекс необходимо периодически ребилдить rebuild
4.
Операции min/max поиска также осуществляются за константное время = высоте дерева (операция index min/max scan) (
BPtree.getMin /
BPtree.getMax )
5. Т.к. данные упорядоченные, то поиск нужного элемента внутри блока происходит с помощью
бинарного поиска (
LNode.getLoc).
Так что если сравнивать время доступа к таблице в 1 блок и к индексу в 1 блок: оба варианта дают 1 физическое чтение с диска, но поиск по индексу будет быстрей, т.к. для поиска элемента в упорядоченном массиве индекса log2(N) операций, а в неупорядоченной таблице - это всегда линейный поиск со стоимостью = N
6. Упорядоченность данных также позволяет
искать данные по диапазону (
BPTree.rangeScan):
* Находим стартовый элемент (
Node.getLoc)
* Двигаемся по блоку вправо (while(leaf != null))
* Если дошли до конца блока, то переходим по ссылке на следующий ( leaf = leaf.next )
* доходим до элемента большего правой границы диапазона (
leaf.keys[i].compareTo(to_key) > 0 )
Это операция последовательного чтения массива, к сожалению, она никак
не может быть распараллелена.
Также если в индексе после столбца, по которому идет сканирование по диапазаону, есть еще столбец, то он не сможет быть использован для доступа к нужному блоку индекса для старта, только для дофильтрации диапазона. Такой метод не уменьшит число физических чтений блоков индекса с диска.
7.
null Значения
Oracle в отличии от других бд не хранит в индексе полностью пустые значения. Это значит что при поиске "idx_cold is null" не будет использоваться.
Это ограничение можно обойти, если создать индекс из 2 полей: нужного и любого другого. В качестве второго поля можно исопльзовать даже константу.
К примеру:
create index idx on tbl(col, 1);
В этом случае все значения колонки col, включая null, будут храниться в индексе и будет работать "col is null" сканирование.
8.
index scip scan
9.
Сжатые индексы
Не релизовывалось в данном классе.
Описание см.
http://blog.skahin.ru/2015/04/oracle.html
10.
Структура блока из 2 столбцов.
[ Flag Byte | Lock Byte | Length Byte 1 | Col1 | Length Byte 2 | Col 2 | Length Byte | rowid ]
Т.е. фактической разницы между индексом из 1 или 2 и более столбцов особо разницы нет.
12.
Фактор кластеризации - соответствие последовательности элементов в индексе элементам в таблице. (
BPtree.getClusterFactor)

Наилучший вариант, когда данные в таблице отсортированы на техже столбцах, что в индексе ( не важно прмямую или обратную). Тогда фактор кластеризации будет равен числу блоков в таблице.
Если же наоборот, то для чтения каждого элемента в индексе нужно считывать новый блок таблицы с диска, тогда фактор кластеризации = числу строк таблицы.
13.
Index full scan - полное сканирование индекса (
BPtree.fullScan)
14.
Index Desc Scan - сканирование в обратном порядке
Индекс строится в прямом порядке и имеет ссылку в листовом блоке только на следующий.
То в случае запроса:
select * from tbl where idx_col between 7 and 9 order by idx_col desc;
Индекс также фильтруется как в п. 6, но обращения к таблице по rowid идет в обратном порядке, т.е. данные повторно не сортируются (order by idx_col desc), т.к. строки уже возвращаются из индекса в обратном порядке.
Исходный код B+дерева на java:
package BPTree;
import java.util.concurrent.ThreadLocalRandom;
public class BPTree<Key extends Comparable, Value> {
//https://en.wikibooks.org/wiki/Algorithm_Implementation/Trees/B%2B_tree
//корень дерева
private Node root;
//кол-во строк в блоке
private final int rows_block;
//высота дерева
private int height = 1;
//кол-во строк в индексе
private int cnt = 0;
public BPTree(int n) {
rows_block = n;
root = new LNode();
//первый блок и последний
root.last = true;
} //BPTree
public void insert(Key key, Value value) {
Split result = root.insert(key, value);
if (result != null) {
//разделяем корень на 2 части
//создаем новый корень с сылками на лево и право
INode _root = new INode();
_root.num = 1;
_root.keys[0] = result.key;
_root.children[0] = result.left;
_root.children[1] = result.right;
//уровень текущей ветки = высота предыдущей + 1
_root.level = result.level + 1;
root = _root;
//повышаем счетчик высоты дерева
height++;
}
} //insert
//index scan
public Value indexScan(Key key) {
Node node = root;
//спускаемся по внутренним веткам, пока не дойдем до листа
while (node instanceof BPTree.INode) {
INode inner = (INode) node;
int idx = inner.getLoc(key);
node = inner.children[idx];
}
//спустились до листа
LNode leaf = (LNode) node;
int idx = leaf.getLoc(key);
//нашли ключ элемента в блоке
//если последний элемент, то дополнительно проверим значение
if (idx < leaf.num && leaf.keys[idx].equals(key)) {
return leaf.values[idx];
} else {
return null;
}
} //indexScan
//index min scan
public Value getMin() {
Node node = root;
//спускаемся по внутренним веткам налево, пока не дойдем до листа
while (node instanceof BPTree.INode) {
INode inner = (INode) node;
node = inner.children[0];
}
if( node.num == 0 ) return null;
//спустились до листа
LNode leaf = (LNode) node;
return leaf.values[0];
} //getMin
//index max scan
public Value getMax() {
Node node = root;
//спускаемся по внутренним веткам направо, пока не дойдем до листа
while (node instanceof BPTree.INode) {
INode inner = (INode) node;
node = inner.children [inner.num];
}
if( node.num == 0 ) return null;
//спустились до листа
LNode leaf = (LNode) node;
return leaf.values[leaf.num - 1];
} //getMax
//index range scan - поиск по диапазону
public Value[] rangeScan(Key from_key, Key to_key) {
Node node = root;
//спускаемся по внутренним веткам, пока не дойдем до листа
while (node instanceof BPTree.INode) {
INode inner = (INode) node;
int idx = inner.getLoc(from_key);
node = inner.children[idx];
}
//спустились до листа
LNode leaf = (LNode) node;
int idx = leaf.getLoc(from_key);
//нашли ключ элемента в блоке
if (idx < leaf.num && leaf.keys[idx].compareTo(from_key) >= 0) {
Value[] arr = (Value[]) new Object[cnt];
//двигаемся вправо, пока не найдем правую границу
int cnt_arr = 0;
do {
//стартуем с найденного элемента
for(int i = idx; i < leaf.num; i++) {
if(leaf.keys[i].compareTo(to_key) > 0) {
//возвращаем только нужное число элементов
Value[] _arr = (Value[]) new Object[cnt_arr];
System.arraycopy(arr, 0, _arr, 0, cnt_arr);
arr = null;
return _arr;
}
arr[cnt_arr] = leaf.values[i];
cnt_arr++;
}
//последующие блоки читаем с 0
idx = 0;
leaf = leaf.next;
} while(leaf != null);
Value[] _arr = (Value[]) new Object[cnt_arr];
System.arraycopy(arr, 0, _arr, 0, cnt_arr);
arr = null;
return _arr;
}
return null;
} //rangeScan
//index full scan
public Value[] fullScan() {
Node node = root;
//спускаемся по внутренним веткам направо, пока не дойдем до листа
while (node instanceof BPTree.INode) {
INode inner = (INode) node;
node = inner.children [0];
}
if( node.num == 0 ) return null;
Value[] arr = (Value[]) new Object[cnt];
//спустились до листа
LNode leaf = (LNode) node;
//последовательно идем по листам слева направо
int cnt_arr = 0;
do {
System.arraycopy(leaf.values, 0, arr, cnt_arr, leaf.num);
cnt_arr = cnt_arr + leaf.num;
leaf = leaf.next;
} while(leaf != null);
return arr;
} //fullScan
//blevel - высота дерева -1
public int getBLevel() {
return height - 1;
} //getBLevel
public int getCnt() {
return cnt;
} //getCnt
//фактор кластеризации
//идеально = число строк / число строк в блоке
//плохо = число строк
public int getClusterFactor() {
int cluster_factor = 0;
int prev_block = 0;
int cur_block = 0;
Object arr[] = new Integer[cnt];
arr = fullScan();
for(int i = 0; i < arr.length; i++) {
int k_rowid = (Integer)arr[i];
cur_block = k_rowid / rows_block;
if(prev_block != cur_block) {
cluster_factor++;
}
prev_block = cur_block;
}
return cluster_factor;
} //getClusterFactor
public void dump() {
System.out.println("blevel = " + getBLevel());
System.out.println("cnt = " + getCnt());
System.out.println("min[k] = " + getMin());
System.out.println("max[k] = " + getMax());
System.out.println("--------------------");
root.dump();
System.out.println("--------------------");
}
//абстрактный класс блока: лист или ветвь
abstract class Node {
//кол-во элементов в блоке
protected int num;
//элементы в блоке
protected Key[] keys;
//высота ветви/листа
int level;
//последний блок ветви/листа
boolean last = false;
//поиск индекса элемента в массиве блока
public int getLoc(Key key, boolean is_node) {
//двоичный поиск в порядоченном массиве O=Log2N
int lo = 0;
int hi = num - 1;
//пока левая и правая границы не встретятся
while (lo <= hi) {
//находим середину
int mid = lo + (hi - lo) / 2;
//если элемент меньше середины
if (key.compareTo(keys[mid]) < 0) {
//если текущий элемент больше, а следующий меньше, то возвращаем текущий
if(mid == 0) return 0;
if(mid > 0 && key.compareTo(keys[mid - 1]) > 0) return mid;
//то верхняя граница - 1 = середина
hi = mid - 1;
} else if (key.compareTo(keys[mid]) > 0) {
//если текущий элемент меньше, а следующий больше, то возвращаем следующий
if(mid == num) return mid;
if(mid < num - 1 && key.compareTo(keys[mid + 1]) < 0) return mid + 1;
//если больше, то нижняя граница = середина + 1
lo = mid + 1;
} else {
//иначе нашли
//для ветви возвращаем следующий за найденным элемент, т.к. ссылка идет налево
if(is_node) return mid + 1;
//для листы чисто найденный элемент
return mid;
}
}
return num;
} //getLoc
// возвращает null, если блок не нужно разделять, иначе информация о разделении
abstract public Split insert(Key key, Value value);
abstract public void dump();
} //Node
//листовой блок дерева
class LNode extends Node {
//ссылки на реальные значения - строки таблицы
final Value[] values = (Value[]) new Object[rows_block];
//ссылка на следующий блок
LNode next;
public LNode() {
keys = (Key[]) new Comparable[rows_block];
level = 0;
} //LNode
public int getLoc(Key key) {
return getLoc(key, false);
} //getLoc
//вставка элемента в листовой блок
public Split insert(Key key, Value value) {
// находим место для вставки
int i = getLoc(key);
//место вставки последний элемент, блок необходимо разбить на 2 части
if (this.num == rows_block) {
/*
* Пример 50/50:
*
3
1 2 3 4 5
---
mid = 5/2 = 2
snum = 4 - 2 = 2 -- уходит направо
mid=2 --уходит налево
keys[mid]=mid[3] = 3 --средний элемент, уходит наверх
* */
//делим блок на 90/10 поумолчанию
int mid = rows_block;
//если вставка идет не в конец
if(!this.last || i < mid) {
//то делим блок 50/50
mid = (rows_block + 1) / 2;
}
//mid = (rows_block + 1) / 2;
//кол-во элементов в правой части
int sNum = this.num - mid;
//новый правый листовой блок
LNode sibling = new LNode();
sibling.num = sNum;
//перемещаем в него половину элементов
System.arraycopy(this.keys, mid, sibling.keys, 0, sNum);
System.arraycopy(this.values, mid, sibling.values, 0, sNum);
//делим ровно на полам, все элементы разойдутся налево или направо
this.num = mid;
//если сплитится последний блок, то помечаем последним правый
if(this.last) {
this.last = false;
sibling.last = true;
}
//позиция в левом блоке
if (i < mid) {
this.insertNonfull(key, value, i);
} else {
//или в правой
sibling.insertNonfull(key, value, i - mid);
}
//информируем блок ветви о разделении: {значение разделения, левый блок, правый блок, 0 уровень листа}
//элемент разделения берем из правой части
Split result = new Split(sibling.keys[0], this, sibling, level);
//связываем текущий блок со следующим
sibling.next = this.next;
this.next = sibling;
return result;
} else {
//блок не полон, вставляем элемент в i мето
this.insertNonfull(key, value, i);
return null;
}
}
//вставка элемента в неполный листовой блок
private void insertNonfull(Key key, Value value, int idx) {
//смещаем все элементы массивов правее idx на 1 элемент
System.arraycopy(keys, idx, keys, idx + 1, num - idx);
System.arraycopy(values, idx, values, idx + 1, num - idx);
//в освободившееся место вставляем элемент
keys[idx] = key;
values[idx] = value;
//число элементов в блоке
num++;
//всего элементов в индексе
cnt++;
}
public void dump() {
if(last) {
System.out.println("(last):");
}
for (int i = 0; i < num; i++) {
System.out.println(keys[i]);
}
}
} //LNode
//класс блока ветви
class INode extends Node {
final Node[] children = new BPTree.Node[rows_block + 1];
public INode() {
keys = (Key[]) new Comparable[rows_block];
} //INode
//поиск индекса для вставки в блоке-ветви
public int getLoc(Key key) {
return getLoc(key, true);
} //getLoc
//вставка элемента в ветвь
public Split insert(Key key, Value value) {
/*
* Упрощенный вариант сплита, когда разделение идет сверху вниз,
* что может привести к преждевременному росту дерева и как следствие дисковых чтений в бд.
* В реальности разделение должно идти снизу вверх - это минимизирует рост дерева.
*
* */
//число элементов в блоке достигло предела - разделяем
if (this.num == rows_block) {
/*
* Пример:
*
2
1 3 4 (3 max)
3
1 2 4 5 (4 max)
---
mid = 5/2 = 2
snum = 4 - 2 = 2 -- уходит направо
mid-1=1 --уходит налево
keys[mid-1]=mid[1] = 2 --средний элемент, уходит наверх
* */
//середина
int mid = (rows_block + 1) / 2;
//создаем блок справа
int sNum = this.num - mid;
INode sibling = new INode();
sibling.num = sNum;
sibling.level = this.level;
//копируем в него половину значений
System.arraycopy(this.keys, mid, sibling.keys, 0, sNum);
//копируем дочерние элементы +1(?)
System.arraycopy(this.children, mid, sibling.children, 0, sNum + 1);
//в левой части будет -1 элемент, он уходит на верхний уровень
this.num = mid - 1;
//передаем информацию о разделении выше: {средний элемент, левая, правая ветвь}
Split result = new Split(this.keys[mid - 1], this, sibling, this.level);
//если элемент меньше середины, то вставляем в левую чать
if (key.compareTo(result.key) < 0) {
this.insertNonfull(key, value);
} else {
//иначе в правую
sibling.insertNonfull(key, value);
}
//информируем вышестоящуюю ветвь о разделении, может ее тоже надо будет разделить
return result;
} else {
//место под разбиение нижних еще есть - вставляем
this.insertNonfull(key, value);
return null;
}
} //insert
private void insertNonfull(Key key, Value value) {
//ищем индекс для вставки
int idx = getLoc(key);
//рекурсивный вызов для нижележайшей ветви
Split result = children[idx].insert(key, value);
//нижний блок пришлось разбить на 2 части
if (result != null) {
//вставка в крайнее правое место
if (idx == num) {
keys[idx] = result.key;
// на нашем уровен становится 2 элемета-ветви
//текущий будет ссылаться на левую чать разделенной дочерней части
//а новый элемент снизу - на правую
children[idx] = result.left;
children[idx + 1] = result.right;
num++;
} else {
//вставка в середину массива
//смещаем все элементы вправа на 1 позицию
System.arraycopy(keys, idx, keys, idx + 1, num - idx);
System.arraycopy(children, idx, children, idx + 1, num - idx + 1);
//аналогично
children[idx] = result.left;
children[idx + 1] = result.right;
keys[idx] = result.key;
num++;
}
} // result != null
} //insertNonfull
public void dump() {
for (int i = 0; i < num; i++) {
children[i].dump();
for(int j = 0; j < level; j++) System.out.print(" . ");
System.out.println("> " + keys[i] + " ("+num+")");
}
children[num].dump();
}
} //INode
//структура с информацией о разделении: значение разделения, левая и правая часть и уровень ветви
class Split {
public final Key key;
public final Node left;
public final Node right;
public final int level;
public Split(Key k, Node l, Node r, int h) {
key = k;
left = l;
right = r;
level = h;
}
} //Split
public static void main(String[] args) {
int rows_on_block = 3;
BPTree t = new BPTree(rows_on_block);
/*for(int i = 0; i <= 99; i++) {
t.insert(i, i);
}*/
/*for(int i = 99; i >= 0; i--) {
t.insert(i, i);
}*/
for(int i = 99; i >= 0; i--) {
t.insert(ThreadLocalRandom.current().nextInt(0, 100), i);
}
// 0 1 2 3 4 5 6 7 8 9 10 11 12 13
/*Integer arr_tst[] = {2, 6, 3, 5, 1, 7, 8, 0, 27, 17, 99, 13, 1, 7};
for(int i = 0; i < arr_tst.length; i++) {
t.insert(arr_tst[i], i);
}*/
t.dump();
System.out.println("indexScan (5) = " + t.indexScan(5));
System.out.println("indexScan (6) = " + t.indexScan(6));
System.out.println("indexScan (4) = " + t.indexScan(4));
System.out.println("indexScan (1) = " + t.indexScan(1));
System.out.println("indexScan (99) = " + t.indexScan(99));
System.out.println("indexScan (100) = " + t.indexScan(100));
Object arr[] = new Integer[t.getCnt()];
arr = t.fullScan();
System.out.print("fullScan = ");
for(int i = 0; i < arr.length; i++) {
System.out.print((Integer)arr[i] + ", ");
}
System.out.println(" ");
System.out.println("cluster_factor = " + t.getClusterFactor());
arr = t.rangeScan(2, 7);
System.out.print("rangeScan(2,7) = ");
for(int i = 0; i < arr.length; i++) {
System.out.print((Integer)arr[i] + ", ");
}
} //main
} //BPTree
Полный код класса и юнит тесты можно посмотреть здесь:
https://github.com/pihel/java/blob/master/BPTree/
 В Oracle для кэширования используется модифицированный алгоритм LRU.
В Oracle для кэширования используется модифицированный алгоритм LRU.
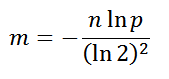

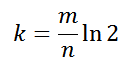
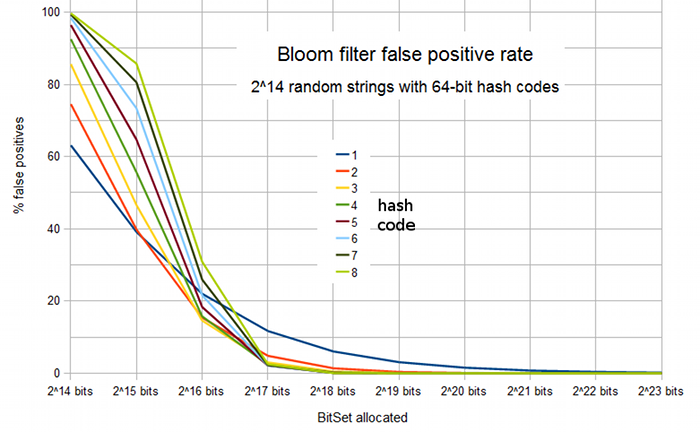
 Коллизии размещаются в томже хэш массиве, но смещаются вправо, пока не найдется свободное место.
Коллизии размещаются в томже хэш массиве, но смещаются вправо, пока не найдется свободное место. Хэш таблица содержит список коллизий. Число элементов хэш таблицы фиксировано = числу различных вариантов хэширующей функции.
Хэш таблица содержит список коллизий. Число элементов хэш таблицы фиксировано = числу различных вариантов хэширующей функции. Слева графически представлен механизм поиска в хэш таблице Oracle.
Слева графически представлен механизм поиска в хэш таблице Oracle.



